The Magic of Adding the Infinitely Small
Integration is one of the most powerful and beautiful tools in mathematics. If differentiation is about breaking things apart to understand their change, integration is about putting things back together to see the whole picture. It’s the bridge between small pieces and the big result from finding the area under a curve to calculating the total distance traveled.
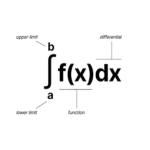
A Brief History Who Founded Integration?
The roots of integration go far back:
Ancient Beginnings: The concept of finding areas and volumes dates back to Ancient Egypt, Greece, and China, where mathematicians used geometric methods.
Eudoxus & Archimedes: In 3rd century BCE Greece, Archimedes developed the method of exhaustion, a precursor to integration, to calculate areas, volumes, and centers of mass.
The Calculus Revolution: In the 17th century, Sir Isaac Newton (England) and Gottfried Wilhelm Leibniz (Germany) independently developed calculus, formalizing integration and its link to differentiation.
Leibniz’s elegant ∫ symbol, derived from the Latin summa (sum), became the universal sign of integration
Interesting Facts about Integration
The integration symbol ∫ is over 300 years old and hasn’t changed since Leibniz introduced it.
Integration can be done exactly (with formulas) or numerically (with computers approximating results).
Without integration, modern physics, engineering, and economics would be impossible.
The word integral comes from Latin integer, meaning whole — because it’s about combining parts into a whole.
Even your phone’s touchscreen sensors use integration to process signals

Real Life Uses of Integration
Integration isn’t just for math classrooms it’s working behind the scenes in everyday life:
Physics: Calculating displacement from velocity, energy from force, or the mass of irregular objects.
Engineering: Designing bridges, buildings, and roads by analyzing loads and stresses.
Economics: Finding total profit, cost, or consumer surplus from rate functions.
Medicine: Determining drug dosage based on rates of absorption.
Astronomy: Calculating the orbits of planets and spacecraft trajectories.
Technology: Graphics rendering in video games uses multiple integrals for realistic lighting and shadows.

Key Applications of Integration
Area Under a Curve: The most famous application, turning complex shapes into measurable quantities.
Volume of Solids: Using methods like disk, washer, and shell integration.
Work & Energy: Computing the total work done by a force over a distance.
Probability & Statistics: Finding probabilities with continuous distributions.
Signal Processing: Filtering and reconstructing audio and image signals.
Why Integration is Fascinating
Integration shows how infinitely small pieces can add up to something big and meaningful. It teaches us that small steps, when combined, create powerful results a lesson as true in life as it is in mathematics.
